Для выполнения практической работы вам потребуется язык программирования Visual Basic. Инструкцию как его установить и где скачать, можно найти в этой теме.

Проект "Диапазон углов" на языке Visual Basic

1. Для создания графического интерфейса проекта "Диапазон углов, обеспечивающих попадание в стенку" разместить на форме:

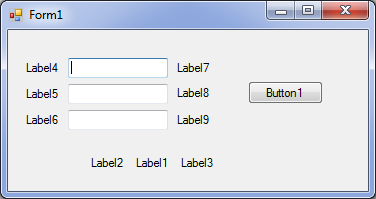
   - три текстовых поля для ввода значений: TextBox1 - начальной скорости, TextBox2 - расстояние до стенки и TextBox3 - высоты стенки;
   - надпись Label1 для вывода диапазона значений углов, при которых происходит попадание мячика в стенку;
   - восемь надписей для обозначения переменных и единиц измерения;
   - кнопку Button1 для запуска обработчика события.

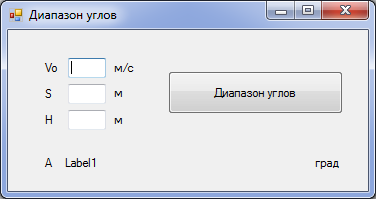
2. Для каждого значения скорости бросания мячика получить диапазон значений углов, обеспечивающих попадание мячика в стенку. Для этого в цикле со счетчиком, которым является переменная А (угол бросания), вычислять высоту мячика в момент его нахождения на расстоянии стенки. Для каждой высоты мячика с помощью оператора условного перехода в сокращенной форме If-Then-End проверять, справедливо ли условие 0<=L And L<=H (попадёт ли мячик в стенку).
Если условие справедливо, то значение переменной А (угол бросания) выводит надпись Label1 с использованием функции преобразования числа в строку Str(A).
Программный код обработчика события:

Const G As Single = 9.81
Const Pi As Single = 3.14
Dim V0, S, H, L As Single, A As Integer
Private Sub Button1_Click(...)
'Ввод начальных значений
V0=Val(TextBox1.Text)
S=Val(TextBox2.Text)
H=Val(TextBox3.Text)
Label1.Text=""
For A=0 To 90
'Попадание в стенку
L=S*Math.Tan(A*Pi/180)-(G*S^2)/(2*V0^2*Math.Cos(A*Pi/180)^2)
'Вывод значений диапазона углов
If 0<=L And L<=H Then
Label1.Text=Label1.Text+Str(A)
End If
Next A
End Sub

3. Запустить проект и ввести скорость бросания мячика, расстояние до стенки и её высоту. Щёлкнуть по кнопке Диапазон углов.

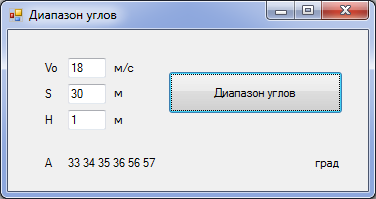
Получим важный результат - оказывается, существуют два диапазона углов: от 33° до 36° и от 56° до 57°, которые обеспечивают попадание мячика при скорости бросания v₀=18 м/с в стенку высотой h=1 м, находящуюся на расстоянии S=30 м.