Для выполнения практической работы вам потребуется пакет программного обеспечения Microsoft Office Excel 2003 и выше.
Проект "Бросание мячика в стенку" в электронных таблицах Microsoft Office Excel
Построение траектории движения мячика
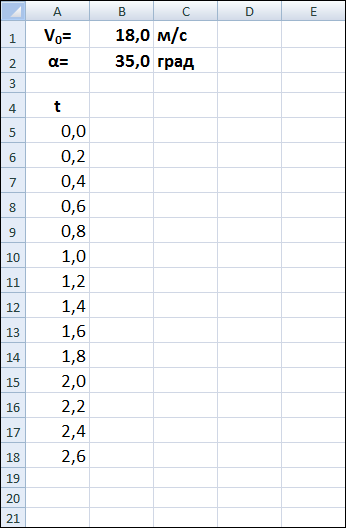
Для ввода начальной скорости бросания мячика v0 будем использовать ячейку B1, а для ввода угла бросания - ячейку B2.

Введём в ячейки A5:A18 значения времени t с интервалом в 0,2 c и вычислим по формулам значения координат тела x и y для заданных значений времени.
В электронных таблицах аргументы функций COS() и SIN() задаются в радианах, поэтому необходимо преобразовать значения углов из градусов в радианы с помощью функции РАДИАНЫ().
1. Ввести:
- в ячейку B5 формулу: =$B$1*COS(РАДИАНЫ($B$2))*A5;
- в ячейку C5 формулу: =$B$1*SIN(РАДИАНЫ($B$2))*A5-4,9*A5* A5;
2. Скопировать введенные формулы в ячейки B6:B18 и C6:C18 соответственно. Получим в столбце B значения координаты мячика по оси X, а в столбце C - координаты мячика по оси Y, вычисленные для определенных моментов времени.
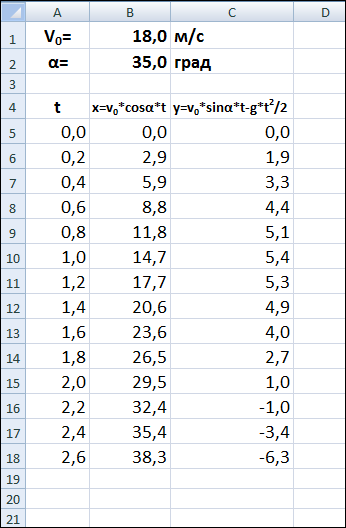
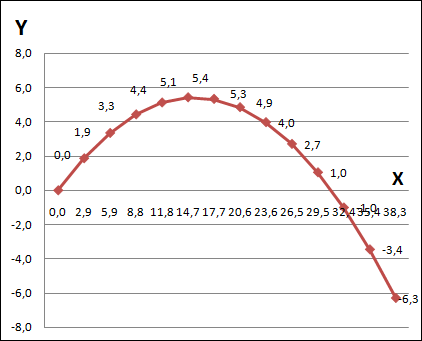
Визуализируем модель, построив график зависимости координаты y от координаты x (траектория движения тела). Для построения движения мячика используем диаграмму типа График.
3. При построении графика в качестве категорий использовать диапазон ячеек B5:B18, а в качестве значений - диапазон ячеек C5:C18.
Компьютерный эксперимент.
Исследуем модель и определим с заданной точностью (например, 0,1°) диапазон углов бросания, которые обеспечивают попадание мячика в стенку.
В качестве начальных условий бросания v0 = 18 м/с, высота стенки h = 1 м, расстояние до стенки s = 30 м.
4. Ввести:
- в ячейку B21 - значение расстояния до стенки;
- в ячейку B22 - значение начальной скорости;
- в ячейку B23 - значение угла;
- в ячейку B25 - формулу для вычисления высоты мячика в момент попадания в стену для заданных начальных условий; =B21*TAN(РАДИАНЫ(B23))-(9,81*B21^2)/(2*B22^2*COS(РАДИАНЫ(B23))^2)
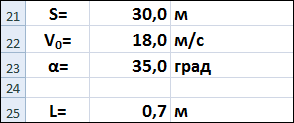
Для заданных начальных условий (скорости бросания и расстояния до стенки) проведем поиск углов, которые дают попадание в стенку на высотах 0 и 1 м. Используем для этого метод Подбор параметра.
Методом Подбор параметра будем сначала искать значение угла бросания, которое обеспечит попадание мячика в стенку на минимальной высоте 0 метров. В данном случае значение функции (высота мячика при попадании в стенку) хранится в ячейке B25, а значение аргумента (угла бросания) - в ячейке B23. Значит, необходимо установить в ячейке B25 значение 0 и методом Подбор параметра найти соответствующее значение аргумента в ячейке B23.
5. Выделить ячейку B25, содержащую значение высоты мячика, и ввести команду [Вкладка: Данные -> Категория: Работа с данными -> Анализ "что-если" -> Подбор параметра...].
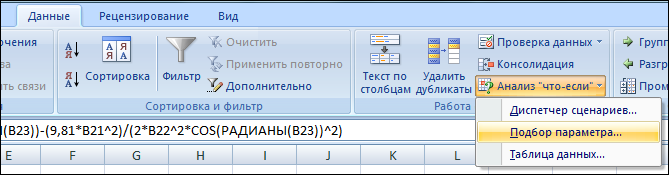
6. В появившемся диалоговом окне ввести в поле Значение: наименьшую высоту попадания в стенку (т.е. 0). В поле Изменяя значение ячейки: ввести адрес ячейки $B$23, содержащей значение угла бросания. Щелкнуть по кнопке ОК.
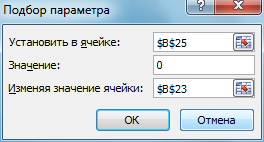
В ячейке B23 появится значение 32,6, т.е. минимальное значение угла бросания мячика, которое обеспечивает попадание в стеку при заданных начальных условиях.
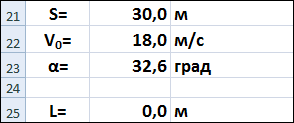
Методом Подбор параметра найдём теперь угол бросания, который обеспечит попадание мячика в стенку на максимальной высоте 1 метр.
7. Выделить ячейку B25, содержащую значение высоты мячика, и ввести команду [Вкладка: Данные -> Категория: Работа с данными -> Анализ "что-если" -> Подбор параметра...].
8. В появившемся диалоговом окне ввести в поле Значение: наибольшую высоту попадания в стенку (т.е. 1).
9. В поле Изменяя значение ячейки: ввести адрес ячейки $B$23, содержащей значения угла бросания.
Щёлкнуть по кнопке ОК.
В ячейке B23 появится значение 36,1, т.е. максимальное значение угла бросания мячика, которое обеспечивает попадание в стенку при заданных начальных условиях.
Анализ результатов. Таким образом, исследование компьютерной модели в электронных таблицах показало, что существует диапазон значений угла бросания мячика от 32,6° до 36,1°, при котором обеспечивается попадание в стенку высотой 1 м, находящуюся на расстоянии 30 м, мячиком, брошенным со скорость 18 м/с.
Если повторить процедуру определения диапазона углов при начальном значении угла в ячейке B23, равном 55°, то получим значения предельных углов 55,8° и 57,4°, т.е. второй диапазон углов.
С учётом точности вычислений в электронных таблицах оба диапазона углов, обеспечивающие попадание в стенку при заданных начальных условиях, совпадают с результатами, полученными при исследовании этой компьютерной модели на языках программирования Visual Basic и Lazarus.