Работа 2.2. Численные эксперименты по обработке звука

Цель работы: знакомство с понятиями «гармонические и негармонические периодические функции» и графическим представлением звуковых колебаний; освоение построения графиков функций в электронных таблицах; получение графической иллюстрации процесса аналого-цифрового преобразования звука.
   Работа носит исследовательский характер и выполняется в самостоятельном режиме.

   Математическая справка. График функции Y(x) — это наглядное (графическое) отображение зависимости значения функции Y от значения аргумента x. График строится в пределах области определения функции (области изменения аргумента х) и области значений Y. Если у функции бесконечная область определения, то для построения графика выбирается тот ее отрезок, в пределах которого поведение функции наиболее характерно. График периодической функции как минимум должен отражать один период изменения значений функции.

Эксперимент 1. Моделирование гармонических колебаний
   Рассмотрим метод построения графика периодической функции, описывающей гармонические колебания.
   Гармоническими колебаниями называются периодические изменения со временем некоторой физической величины, описываемые функциями синуса или косинуса. Общая запись такой функции:

Y=A*sin(2πvt+ⱷ) или Y = A*cos(2πvt+ⱷ),

где А — амплитуда колебаний, t — время (аргумент функции), v — частота колебаний, Гц, ⱷ — начальная фаза колебаний.
   Период функций sin и cos равен 2π. Значение функции Y изменяется в интервале от -А до +А. График функции синуса называют синусоидой.
   Звуковые колебания, описываемые гармонической функцией, называют гармоническими колебаниями. Чистые музыкальные тона — до, ре, ми и др. — представляют собой гармонические звуковые колебания разной частоты. Такие гармонические звуковые колебания издает камертон — эталонный источник музыкального тона. Гармонические колебания совершает также математический маятник, а в электрическом колебательном контуре сила тока периодически изменяется по гармоническому закону.
   Рассмотрим метод построения графика гармонической функции в среде электронных таблиц (на примере табличного процессора MS Excel).
   Работа проходит в два этапа:
1) табулирование функции (построение таблицы значений функции на некотором интервале значений аргумента с постоянным шагом);
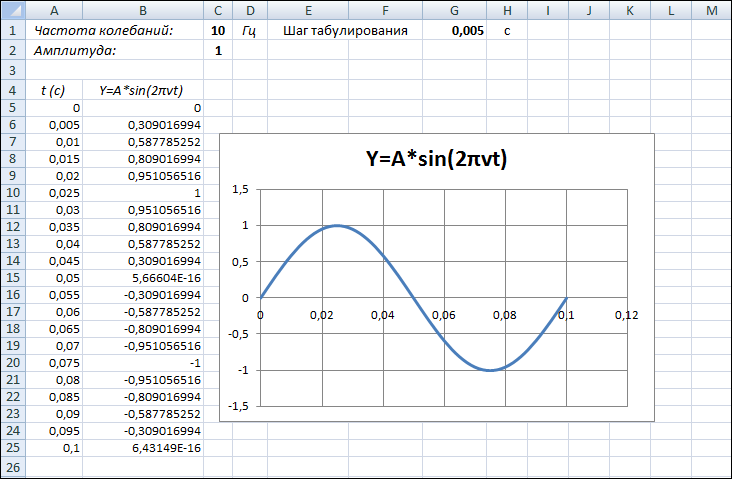
2) построение графика функции. Получаемая при этом электронная таблица представлена на рисунке ниже.
   Параметрами функции являются частота колебаний v и амплитуда А. Их значения вводятся, соответственно, в ячейки C1 и C2.
Значение начальной фазы ⱷ примем равным нулю.

   Шаг табулирования записан в ячейке G1.
   Таблица размещена в ячейках А4:В25. В столбце А расположены значения аргумента (времени t), в столбце В — значения функции У = А * sin(2πvt+ⱷ).
   Изменение времени начинается со значения t = 0 (ячейка А5). В ячейке А6 записана формула =A5+$G$1, которая затем копируется в последующие ячейки столбца А. Таким способом обеспечивается изменение значения времени t с постоянным шагом Δt, хранящимся в ячейке G1.
   В ячейку В5 заносится формула =$C$2*SIN(2*ПИ()*$C$1*A5), вычисляющая значение функции от аргумента, записанного в ячейке А5. Стандартная функция ПИ() при этом возвращает значение числа Пифагора — π. Формула из ячейки В5 копируется вниз по столбцу до ячейки В25.
   На рисунке ниже показаны результаты табулирования функции для значений = 10 Гц, А = 1. Шаг табулирования принят равным 0,005. При частоте 10 Гц период колебаний равен 1/10 = 0,1 с. При шаге табулирования 0,005 на одном периоде укладывается 20 шагов — это вполне достаточное количество значений для построения графика функции.

   Построение графика. Для графической обработки данных в табличном процессоре имеется Мастер построения диаграмм и графиков. Его вызов осуществляется при помощи меню Вставка, Диаграммы. Дальнейшие шаги построения графика следующие:
   1) выбор типа диаграммы: стандартные, точечная, вид - сглаживающие линии;
   2) задание диапазона данных (значений функции): в столбцах - В5:В25; на вкладке Ряд - значения X: А5:А25;
   3) ввод заголовка: «Y = A*sin(2πvt+ⱷ)» и подписей под осями: «t», «Y», включение линий сетки, отключение вывода легенды и подписей данных;
   4) выбор, на каком листе рабочей книги построить диаграмму.
   После нажатия кнопки Готово график будет построен.
   Толщину линий, цвет фона, вид координатной сетки и другие параметры оформления графика можно настроить отдельно, используя контекстное меню (раскрываемое щелчком правой кнопки мыши) и задавая нужные значения для соответствующих объектов.

   Человек слышит звуковые колебания, в среднем в диапазоне частот от 20 Гц до 20 кГц. Частоте 10 Гц соответствует инфразвук. Некоторые животные способны воспринимать его на слух. Если удвоить эту частоту, то будет достигнута нижняя частотная граница слышимости звука человеком. Тогда на временном интервале 0,1с. поместится два периода колебаний.
   Такой эксперимент легко выполнить на уже построенной электронной таблице. Измените значение частоты в ячейке C1 на 20, после чего таблица будет автоматически пересчитана, а график примет вид, представленный на рисунке.

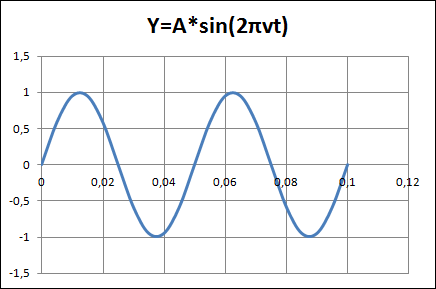
   На интервале времени 0,1 c здесь, как и предполагалось, укладывается два периода функции. Следовательно, период колебаний равен 0,05 с.

Электронные таблицы

   Задание 1 (уровень 1). Проведите несколько экспериментов с электронной таблицей для следующих значений частоты: 5 Гц, 15 Гц, 30 Гц, 40 Гц. В каждом случае определите, сколько периодов колебаний укладывается на интервале 0,1 с.

Эксперимент 2. Моделирование негармонических колебаний

В разделе математики, который называется гармоническим анализом, доказано, что любую периодическую функцию Y(t) с частотой v можно представить в виде суммы гармонических (синусоидальных) функций с частотами v, 2v, 3v, 4v ... . Такие слагаемые называют гармониками, а представление функции в виде суммы гармоник называют ее гармоническим разложением:

Y(t)=A₁*sin(2πvt+ⱷ₁) + A₂*sin(4πvt+ⱷ₂)+ A₃*sin(6πvt+ⱷ₃)+…,

где A₁, А₂,…- амплитуды гармоник, а ⱷ₁, ⱷ₂ … — начальные фазы гармоник. Количество слагаемых для некоторых таких функций может быть конечным, но в общем случае оно бесконечно.
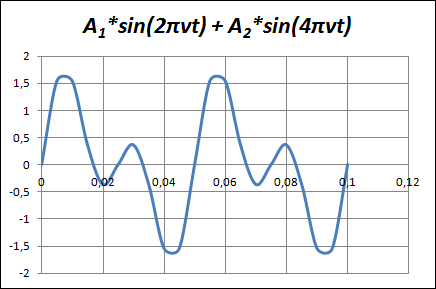
   Пример. Построим график негармонической периодической функции, представленной в виде суммы двух гармоник:

Y(t)=A₁*sin(2πvt) + A₂*sin(4πvt)

   Начальные фазы здесь равны нулю. Выполним расчеты для следующих значений параметров: v = 20 Гц, А₁ = А₂ = 1. Как было сделано ранее, вычисления мы будем производить на отрезке времени от 0 до 0,1 с, а шаг табулирования выберем равным 0,005.
   Для получения нужной таблицы значений достаточно заменить содержимое ячейки В5 на следующую формулу:

=$C$2*SIN(2*ПИ()*$C$1*A5)+$C$2*SIN(2*ПИ()*2*$C$1*A5),

а затем скопировать эту формулу вниз по столбцу В.
   Получаемый график  представлен на рисунке ниже. Из него видно, что период колебаний равен 0,05 с, т. е. периоду первой гармоники. Максимальная амплитуда колебаний увеличилась и стала равна приблизительно 1,54.

Электронные таблицы

   Задание 2 (уровень 1). Получите график колебаний, который отличается от рассмотренного выше тем, что амплитуда второй
гармоники в два раза меньше, чем первой: А₂ = А₁/2.
   Задание 3 (уровень 2). Получите график колебаний, складывающихся из трех гармоник со следующими параметрами: А₁ = 1, v₁ = 20 Гц; А₂ = A₁/2, v₂ = 2₁; А₃ = А₂/2, v₃ = 2₂. Начальные фазы равны нулю.
   Задание 4 (уровень 2). Получите график колебаний, складывающихся из двух гармоник с параметрами: А₁ = 1, V₁ = 20 Гц, ⱷ₁ = 0; А₂ = A₁, v₂ = 2v₁, ⱷ₂ = π/2. Сравните полученный график с рисунком выше. Сделайте вывод: как сдвиг фаз между гармониками повлиял на амплитуду колебаний? На период колебаний?

Эксперимент 3. Моделирование аналого-цифрового преобразования

В этом эксперименте моделируется процесс аналого-цифрового преобразования (АЦП). Он включает в себя дискретизацию сигнала по времени и квантование значений амплитуды сигнала.
   Дискретизация по времени определяется значением частоты дискретизации Н (Гц). Шаг по времени между двумя измерениями равен 1/Н с.
Процесс квантования амплитуды определяется параметром глубины квантования звука b: количество уровней квантования равно 2^b. Коды, определяющие амплитуду звукового сигнала, - это целые числа в диапазоне от 0 до 2^b.

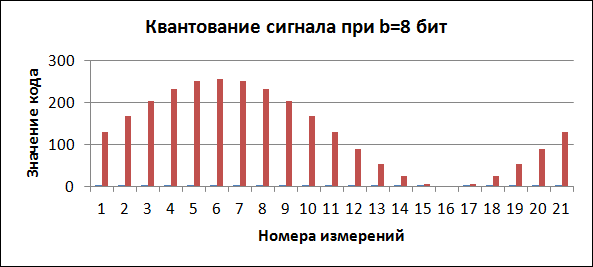
   Модель процесса квантования звукового сигнала, реализованная в среде электронных таблиц, представлена на рисунке ниже.
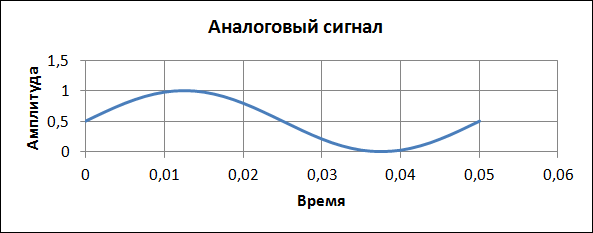
Рассматривается гармонический сигнал с частотой v = 20 Гц (ячейка C1). Частота дискретизации АЦП Н = 200 Гц (ячейка C2).
Глубина квантования b = 8 бит (ячейка G2).
   Столбец А содержит значения моментов времени измерений сигнала при реализации АЦП. В ячейке А5 записан начальный момент времени t = 0, далее время увеличивается с шагом 1/Н с.
В ячейке А6 записана формула =A5+1/$C$2, которая далее скопирована вниз по столбцу А.
   Значение амплитуды аналогового сигнала вычисляется по формуле:

Y = 0,5(1 + sin(2 πvt)).

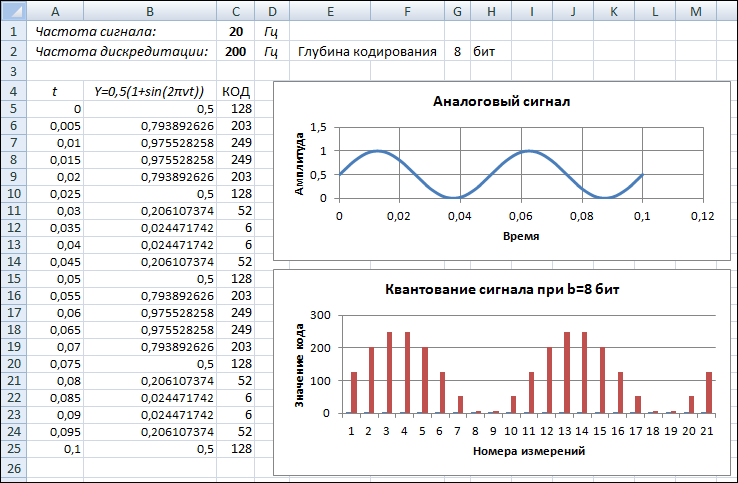
   Такое преобразование синусоиды переносит ее в область положительных значений Y в интервале от 0 до 1 (это сделано для упрощения описания дальнейшего процесса квантования). Соответственно, в ячейку В5 записана формула =(1+SIN(2*ПИ()*$C$1*A5))/2, которая затем скопирована вниз по столбцу В.
   В столбце С получены коды измерений амплитуды сигнала, представленные целыми десятичными числами (при записи в память компьютера в ходе реального алфавитно-цифрового преобразования они переводятся в двоичную систему счисления).
   В ячейку С5 помещена формула =ЦЕЛОЕ(B5*2^$G$2). Ее смысл следующий: поскольку Y лежит в диапазоне от 0 до 1, значение выражения [Y * 2^b] будет равно целым числам в диапазоне от 0 до 2^b (квадратные скобки обозначают выделение целой части числа).
   При построении диаграммы «Квантование сигнала» следует выбирать тип Гистограмма, дискретный вид которой наглядно отражает дискретный характер кода. Таблица построена в расчете на 21 измерение сигнала; при заданных значениях v и Н удалось
«оцифровать» два периода колебаний сигнала.
   При изменениях трех параметров модели: v, Н и b производится автоматический пересчет таблицы. Например, если увеличить частоту дискретизации в два раза, т. е. занести в ячейку С2 число 400, то мы получим графики, представленные на рисунках ниже.
   Здесь измерения произведены на одном периоде колебаний, зато дискретный код более подробно описывает колебательный процесс.
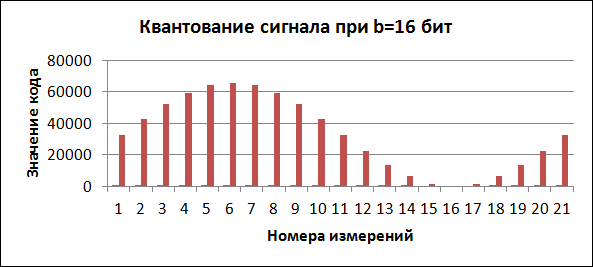
   Гистограмма квантования на рисунке ниже получена для значения b = 16. На этом рисунке видно, что диапазон значений кода увеличился, следовательно, такое кодирование дает более точную информацию о величине сигнала, чем при b = 8.

Электронные таблицы

   Задание 5 (уровень 1). Проведите расчеты при значениях параметров: v = 20 Гц , Н = 100 Гц, b = 8 бит. Сопоставьте полученные результаты с этими:

   Сделайте выводы.

   Задание 6 (уровень 2). Проведите численные эксперименты по кодированию негармонических колебаний. Функции, описывающие негармонические колебания, возьмите из заданий к эксперименту № 2.

   Программирование на Паскале
   Задание 7 (уровень 3). Составьте программу на Паскале, моделирующую процесс кодирования аналогового сигнала (без рисования графиков). Программа должна воспроизводить таблицы, которые были получены выше в среде табличного процессора.

---

Используемая литература:
Информатика. Углубленный уровень: практикум для 10-11 классов : в 2 ч. Ч. 1 / И. Г. Семакин, Т. Ю. Шеина, Л. В. Шестакова. - М.: БИНОМ. Лаборатория знаний, 2013. - 168 с. : ил.