Дубликат урока: Перейти

Составить оптимальный план проведения экскурсионных поездок школьников во время каникул в следующей ситуации. Областной департамент образования может профинансировать поездки школьников из пяти районов области (районы будем обозначать номерами) в три города (назовем эти города X, У и Z).

   Количество учащихся, которых следует отправить в поездки, таково:

   Экскурсионное бюро может в данные каникулы обеспечить поездку следующего количества учащихся в каждый из трех городов:

   Стоимость поездки (в рублях) приведена в следующей таблице.

   Смысл чисел в таблице таков: если в ячейке Y2 стоит 600, то это значит, что поездка одного учащегося из района 2 в город У обходится в 600 рублей.
   Необходимо составить такой план экскурсий, который бы:
   • позволил каждому из намеченных к поездке учащихся побывать на экскурсии;
   • удовлетворил условию об общем числе экскурсантов в каждый из городов;
   • обеспечил максимально низкие суммарные расходы финансирующей стогны.

   Поскольку эта задача непроста, поможем вам с ее математической формулировкой.

   План перевозок, который нам надлежит составить, будет отражен в следующей таблице:

   Величины, стоящие в этой таблице, и являются объектами поиска. Так, x3 есть число учащихся из района № 3, которые по разрабатываемому плану поедут в город X.
   Первое условие (ограничение задачи) состоит в том, что все учащиеся из каждого района поедут на экскурсию. Математически оно выражается следующими уравнениями:

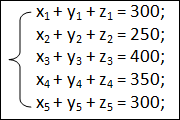
   Второе условие — в каждый город поедут столько учащихся, сколько этот город в состоянии принять:

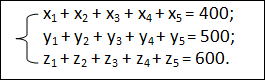
   Кроме того, искомые величины, разумеется неотрицательны:

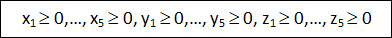
   Теперь запишем общую стоимость расходов на экскурсии. Поскольку привести, например, на экскурсию X1 учащихся в целом стоит X1-500 рублей (см. таблицу стоимости поездки), то общие расходы составят:

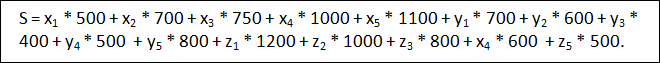
   Теперь имеется всё для полной математической формулировки задачи: требуется найти наименьшее значение функции (4) при условии, что входящие в нее переменные удовлетворяют системам уравнений (1) и (2) и неравенств (3).

   Это весьма непростая задача. Однако ее решение (как и задач, существенно более сложных) вполне «по плечу» программе Excel с помощью средства Поиск решений, которым вам и надлежит воспользоваться.

   Приведем результат решения задачи:

   Итог: в город X поедут на экскурсию 300 учащихся из района №1 и 100 учащихся из района № 2, в город Y — 100 учащихся из района № 2 и 400 из района № 3, в город Z — 50 учащихся из района № 2, 350 — из района № 4 и 200 — из района № 5.
   Полученный результат можно сформулировать следующим образом:
   все учащиеся из района № 1 уедут в город X, учащиеся из района № 2 поделятся между городами X, Y и Z (соответственно 100, 100 и 5), все учащиеся из района № 3 уедут в город Y, а все учащиеся из районов № 4 и № 5 поедут в город Z. Такое неочевидное, на первый взгляд, разделение обеспечивает в данном случае наибольшую экономию средств.